問1 A,B,C,Dを論理変数とするとき、次のカルノー図と等価な論理式はどれか。ここで、・は論理積、+は論理和、XはXの否定を表す。
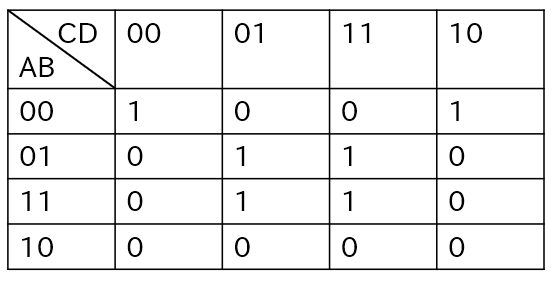
出典: 令和4年度 秋期 エンベデッドシステムスペシャリスト試験 午前I 問1
ア A・B・C・D+B・D
イ A・B・C・D+B・D
ウ A・B・D+B・D
エ A・B・D+B・D
解説
選択肢で気になったのは、すべて~+~の形式になっていることと、すべてにB・Dがあることです。
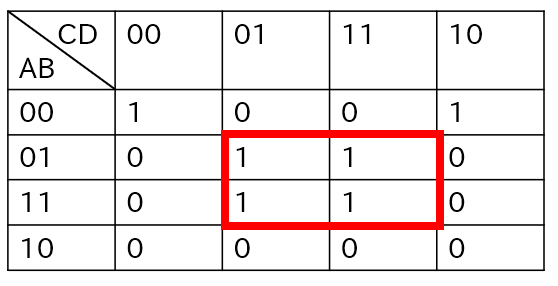
カルノー図のB、Dを見て気づくのは赤枠の内側がB=1かつD=1のときに結果が1となっていることです。
つまり、赤枠の外側がすべて0だとしたらB・Dという論理式になるはずです。
上のカルノー図からB・Dとの論理和を除外すると以下のようになります。
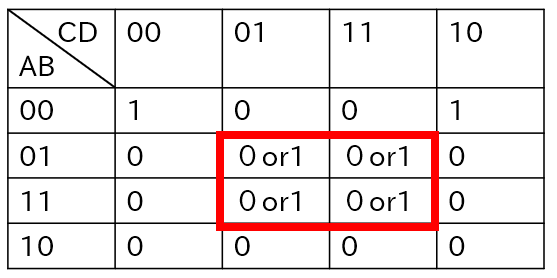
赤枠の内側は0でも1でもどちらでも良いことになります。
つぎは、以下の赤枠に注目してみました。
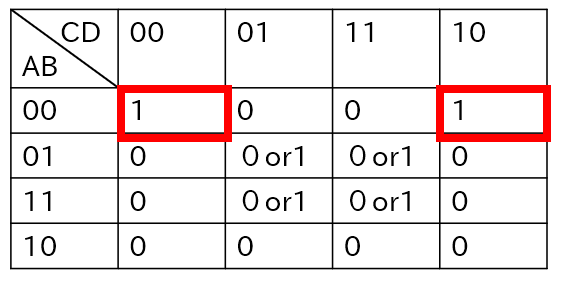
この赤枠は、A=0かつB=0かつD=0のときに1という結果になっています。
つまり、赤枠の外側がすべて0だとしたらA・B・Dという論理式になるはずです。
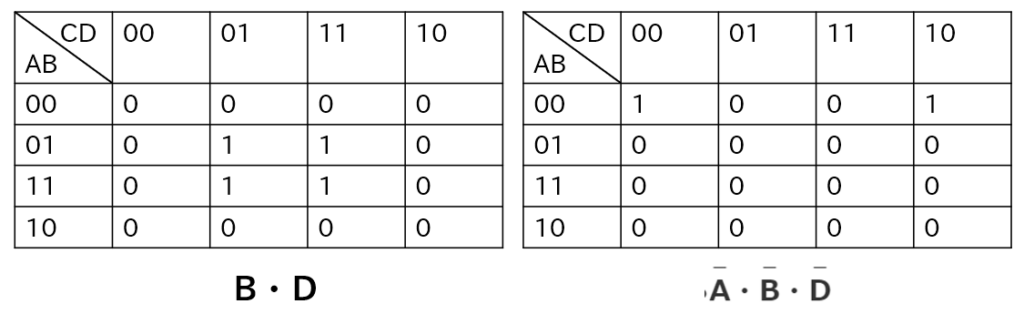
A・B・DとB・Dの論理和を求めると問題のカルノー図と一致します。
答えは、エ A・B・D+B・D となります。


コメント